AAAI 2025 | 用于韦伯区位问题的去奇异性次梯度方法

本文提出一种解决奇异性问题的直观方法。

原标题：AAAI 2025 | 用于韦伯区位问题的去奇异性次梯度方法
文章来源：机器之心
内容字数：7070字

暨南大学通用机器学习课题组在韦伯区位问题研究取得突破

本文报道了暨南大学通用机器学习课题组在解决韦伯区位问题奇异性问题上的最新研究成果。该课题组由网络空间安全学院和信息科学技术学院的多名师生组成，研究方向涵盖通用逼近理论、分布外泛化、非凸优化等多个领域。2024年4月至12月，课题组已在ICML、NeurIPS、IJCAI、AAAI等顶级会议上发表5篇论文。

1. 韦伯区位问题及奇异性挑战

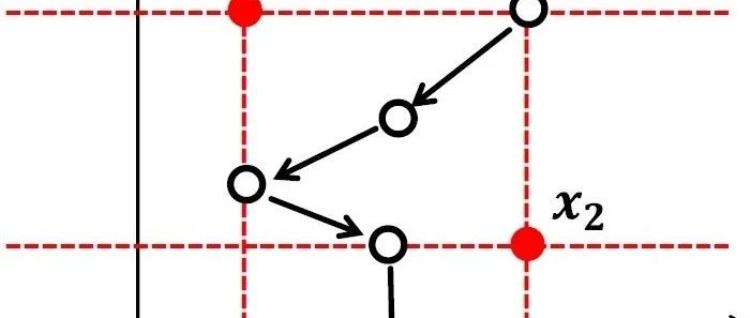
韦伯区位问题旨在寻找一个中心点，使其到多个给定点的加权距离之和最小。该问题广泛应用于机器学习、人工智能等领域。其目标函数包含两个参数：距离范数的p值和距离幂次q值。当1≤q≤p且1≤p<2时，目标函数存在奇异性问题，即梯度在某些点不存在，算法可能陷入奇异集而无法收敛。此前的研究主要针对p=2的情况，而1≤p<2的情况更为复杂，奇异集包含无限多个点。

2. 去奇异性次梯度法

为了解决这一问题，课题组提出了一种名为“去奇异性次梯度法”的全新方法。该方法通过识别引发奇异性的数据点和维度，去除相应的分量，从而构造出一种新的次梯度。该次梯度具有良好的性质，例如能够刻画最小值点和下降方向。基于此，课题组构建了一种名为qPpNWAWS的算法，该算法在非奇异情况下使用常规Weiszfeld迭代，在奇异情况下使用沿下降方向的线性搜索法，保证损失函数持续下降并最终收敛。

3. 算法性能及实验结果

课题组在CSI300数据集上进行了实验验证。实验结果表明，qPpNWAWS算法在奇异点通常只需不超过3次线性搜索即可使损失函数下降，总迭代次数和时间分别不超过15次和0.02秒，并达到线性收敛速度。此外，在在线资产配置实验中，该算法在某些(q,p)组合下取得了比原始版本(q,p)=(1,2)更高的投资得分。

4. 通用机器学习研究方向

该研究属于通用机器学习领域的基础模块开发和优化器开发方向。课题组近期还在深度学习框架、分布外泛化、逼近理论、稀疏学习等方向取得了其他重要成果，例如在ICML和NeurIPS发表的关于不变风险最小化和稀疏投资组合优化的论文。

5. 结论

暨南大学通用机器学习课题组提出的去奇异性次梯度法有效解决了韦伯区位问题在1≤q≤p且1≤p<2情况下的奇异性问题，为该问题的求解提供了新的思路，并具有重要的实际应用价值。该研究成果已发表在arXiv上，论文链接为：http://arxiv.org/abs/2412.15546，项目地址为：https://github.com/laizhr/qPpNWAWS。

联系作者

文章来源：机器之心
作者微信：
作者简介：专业的人工智能媒体和产业服务平台