微积分的奇妙之旅：从零到无穷的探索之路

原标题：从一到无穷∞微积分从娃娃学起
文章来源：量子学派
内容字数：5190字

微积分的魅力与核心思想

微积分是一门关于简化与累积的学科，通过将复杂现象分解为无数小片段，最终再将这些片段重新累加，以帮助我们理解自然界中的复杂现象。

1. 无穷小的概念

无穷小是一个无限接近于零但不等于零的概念。通过测量不同尺度的物体，我们可以看到无穷小在微积分中的重要性。它有助于我们理解许多数学现象和悖论，例如飞矢不动悖论和乌龟悖论，这些悖论挑战了我们的直觉。

2. 穷竭法与早期微积分

古希腊数学家利用“穷竭法”探索如何计算圆形的面积，通过不断分割和累积，将多边形的面积无限接近于圆的面积。刘徽的割圆术和阿基米德的估算方法为微积分的发展奠定了基础。

3. 切割与累积的基本思想

微积分的核心概念是微分与积分，它们依赖于无穷小的切割和累积。微分表示函数的瞬时变化率，而积分则表示无穷小变化的累积。

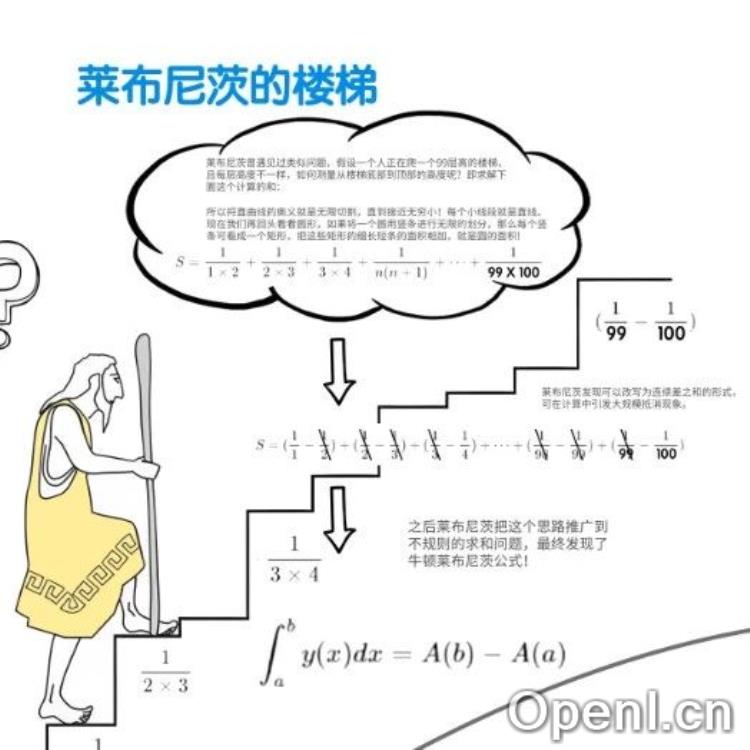
4. 莱布尼茨的楼梯法

莱布尼茨通过“楼梯法”推导出连续求和的公式，展示了如何将复杂问题转化为简单的连续差分之和。这一方法的核心在于将低维复杂问题提升到高维度进行思考。

5. 微积分的基本定理

微积分的基本定理将连续变化的函数转化为更高维度的累积函数，从而简化了复杂问题的解决过程。这种思想不仅是一个计算工具，更是一种观察和理解世界的方法。

6. 定积分的应用

微积分的强大在于它能够将复杂的连续变化转化为简单的公式，帮助我们求解面积、体积和位移等问题。无论多么复杂的现象，微积分都能提供有效的描述和计算方式。

总结

微积分以无穷小和高维累积的概念为基础，通过简化复杂的变化过程，帮助我们更精确地理解和计算自然界的规律。它不仅是一种数学工具，更是观察和理解世界的重要方法。

联系作者

文章来源：量子学派
作者微信：
作者简介：专注于科普（数理哲）的教育平台，“典赞·2019科普中国”十大科普自媒体